Monthly Archives: March 2012

How to Model with Bayesian Networks

Posted on by
2

—Ann E Nicholson

Since Bayesians without Borders will in significant part be about Bayesian networks and their uses, in this post I will introduce them to newcomers to the technology.

Bayesian networks (BNs) are an increasingly popular technology for representing and reasoning about problems in which probability plays a role. A Bayesian network is a directed, acyclic graph whose nodes represent random variables and arcs represent direct dependencies. The arcs often, but not always, also represent direct causal connections between the variables. The nodes pointing to X are called its parents and collectively are denoted \pi(X). The relationship between variables is quantified by conditional probability tables (CPTs) associated with each node, namely P(X|\pi(X)). The CPTs together compactly represent the full joint distribution. Users can set the values of any combination of nodes in the network that they have observed. This evidence, e, propagates through the network, producing a new posterior probability distribution P(X|e) for each variable in the network. There are a number of efficient exact and approximate inference algorithms for performing this probabilistic updating, providing a powerful combination of predictive, diagnostic and explanatory reasoning.

I will illustrate with the design of a BN for a simplified version of a real ecological problem, modeling native fish populations in Victoria. Problem: A local river with tree-lined banks is known to contain native fishpopulations, which need to be conserved. The river passes through croplands and is susceptible to drought conditions. Rainfall helps native fish populations by maintaining water flow, which increases habitat suitability as well as connectivity between different habitat areas. However, rain can also wash pesticides that are dangerous to fish from the croplands into the river. What we want to do is build a BN adequate for modeling this system.

The first step is to decide what the variables of interest are, which will become the nodes in the BN. The abundance of native fish directly depends only on the level of pesticide in the river and the river flow, hence Native Fish Abundance — a so-called "leaf node" — has only those two parent nodes. RiverFlow depends on how much rain falls in a given year (Annual Rainfall), and how much of that water ends up in the river, which means it depends also on the long term Drought Conditions. The amount of pesticide in the river (Pesticide in River) depends on Pesticide Use and whether there is enough rain (Annual Rainfall) to wash it into the river. Finally, the condition of the trees on the river bank depends only on the long term drought and more recent rainfall.

This graphical structure captures these causal interactions: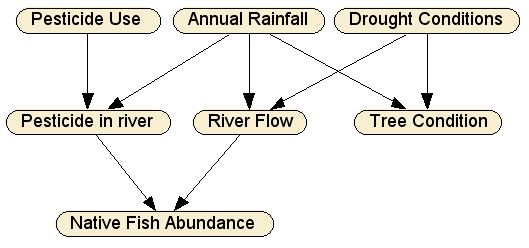

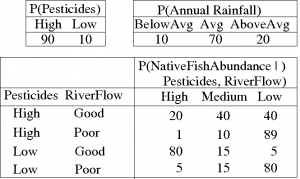
In consultation with an ecologist we might build the CPTs (i.e., eliciting the parameters from the ecologist), as in these example tables:

Note that Pesticide Use (just "Pesticides" in the table) and Annual Rainfall are so-called "root nodes" with no parents, so there is only a single probability distribution for each, whereas for nodes with parents there is a conditional distribution for each possible instantiation of its parents.

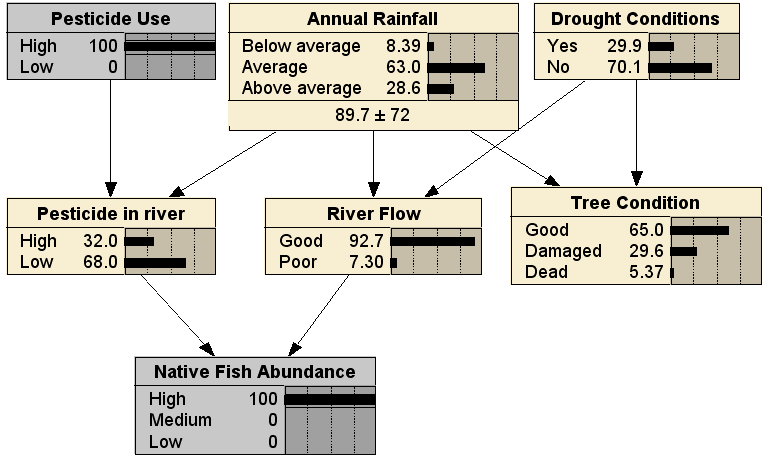
The CPT for the Native Fish Abundance node shows the possible combinations of values for the parent nodes (Pesticides and River Flow), and a probability distribution of the resultant Native Fish Abundance, over the three levels, High, Medium and Low. We can see that the best conditions for the fish are Low levels of pesticide and Good River Flow (.8, .15, 0.05), while the worst are High pesticide use and Poor River Flow (.01, .10, .89). Note also that there may well be other factors in play, such as the presence of exotic predators, or disease, that are not represented explicitly by nodes in the BN. The effects of these are averaged over in the CPTs. They are reflected, for example in the 0.05 probability that native fish abundance is Low, even under the best pesticide and river flow conditions.

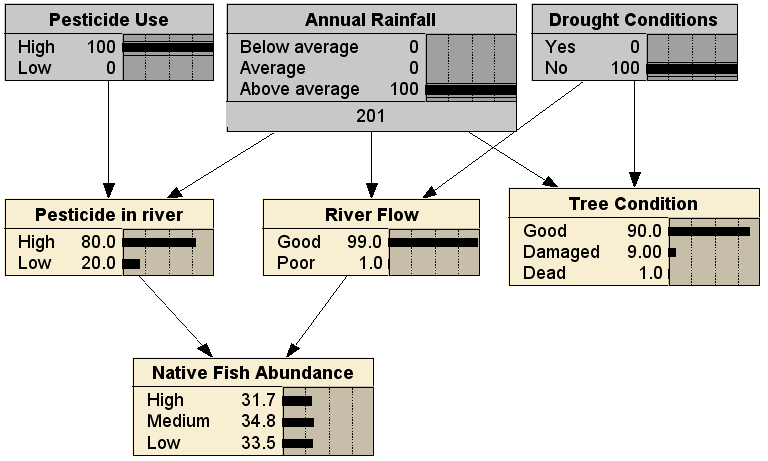
Now that we have the BN structure and its parameters, the BN can be used for reasoning. That is, we can instantiate different possible scenarios by updating the values of particular nodes and then updating the BN, using one of the many Bayesian network programs around, such as Netica. First, here is the network with no evidence:

 

Without making any observations, this BN tells us that the most likely state of the native fish is Low abundance (57.8%), though the Tree Condition is most likely Good (53.3%). If we add observations of the root nodes in the BN, when there is High pesticide use, above average rainfall and no drought conditions, we get:

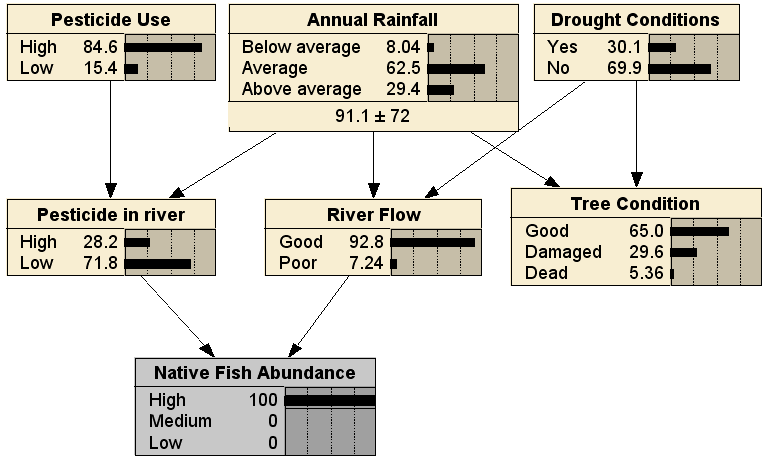
This reasoning is predictive, from cause to effect. In this scenario, the prediction is that the Native Fish Abundance will improve, due to the River Flow being Good, despite the increased Pesticide in River. Alternatively, the BN can be used for diagnosis, by entering evidence for the Native Fish Abundance leaf node:

Comparing to the no evidence case, we can see that it is less likely that the pesticide use was high, less likely there have been drought conditions, and more likely that rainfall has been above average. Finally, we can use the BN in any arbitrary combination of diagnostic and predictive reasoning; here with evidence entered for both a cause (Pesticide Use being High) and an effect (Native Fish Abundance being High), resulting in (fairly small) changes to the distributions for all the other nodes:

Here I have briefly described and illustrated the usual knowledge engineering process of building Bayesian networks. There is, of course, a great deal more to it when building a real network of any complexity, which you can read about in depth in our book Bayesian Artificial Intelligence. Some of these, including causal discovery algorithms for learning BNs from sample data, will also be discussed in future posts in this blog.

Sally Clark is Wrongly Convicted of Murdering Her Children

Posted on by
5

— Kevin B Korb†

Sally Clark, in an infamous miscarriage of justice, was convicted of murdering her two sons in the UK in 1999 after a prosecution which employed primarily statistical reasoning in a way that has become notorious as the "prosecutor's fallacy". Here I will briefly review the arguments and the statistical reasoning from a Bayesian perspective. I don't propose the details of this analysis (i.e., the exact probabilities) be taken too seriously. They are taken from fairly cursory searches on the Internet and applied in a fairly crude way. Regardless, they are far more serious than anything produced during the trial itself!

Sally Clark was arrested after her second baby died a few months old, apparently of sudden infant death syndrome (SIDS), exactly as her first child had died a year earlier. According to prosecution testimony (by a pediatrician, Sir Roy Meadow), about 1 in 8543 babies die of SIDS. They argued that there is only a probability of \lgroup \frac{1}{8543} \rgroup^2 \approx 1/73000000 that two such deaths would happen in the same family by chance alone (after controlling for tobacco smoke and a few social factors). According to the prosecution, the woman was guilty beyond a reasonable doubt. The jury returned a guilty verdict, even though there was no substantial evidence of guilt presented beyond this argument.

Let h = Clark is guilty, e1 = the evidence of the first son's death, e2 = the evidence of the second son's death. Note that the latter two are meant to establish the appearance of SIDS deaths. Then the prosecutor's argument was:

  1. P(e1|\neg h) = P(e2|\neg h) = \dfrac{1}{8543}
  2. So, P(e1 \wedge e2|\neg h) \approx P(e1|\neg h) \times P(e2|\neg h) \approx 1/73000000
  3. So, P(h|e1 \wedge e2) = 1 - 1/73000000 \approx 1

There are a lot of problems with this argument. Here I will discuss the two most basic errors, which probably have the most impact and which anyone involved with assessing evidence should be capable of recognizing. First, the combination of the evidence in (2), simply by multiplication, requires the two pieces of evidence to be independent of each other. The general form of such a combination is P(e1 \wedge e2|\neg h) = P(e1|\neg h) \times P(e2|e1,\neg h), which further reduces to (2) only if P(e2|\neg h) = P(e2|e1,\neg h), that is, only if the two items of evidence are independent given innocence. However, risk factors for SIDS are very likely to be common to multiple children within a family, including not the just tobacco smoke and the social factors controlled for, but also poor prenatal care, low birth weights, alcohol consumption and sleeping practices (and, to be sure, physical abuse by parents). In any case, one SIDS death is well known to raise the probability of another in the family;‡ therefore, the combined evidence of two deaths must have a higher probability than their simple multiplication. One study reported a relative risk of recurrence of SIDS of 5 times the background rate, a rate found to be comparable to other recurrent mortality risks in siblings. This yields P(e1 \wedge e2|\neg h) = P(e1|\neg h) \times P(e2|e1,\neg h) = 1/14.7M, instead of 1/73M.

The second failure in the prosecution argument is the complete neglect of prior probabilities. Bayes' rule says:

  • P(h|e1 \wedge e2) = \dfrac{P(e1 \wedge e2|h)P(h)}{P(e1 \wedge e2)}
  • P(h|e1 \wedge e2) = \dfrac{P(e1 \wedge e2|h)P(h)}{P(e1 \wedge e2|h)P(h) + P(e1 \wedge e2|\neg h)P(\neg h)}
For simplicity, I will assume that P(e1 \wedge e2|h) = 1, i.e., that guilt would surely produce the evidence found. But, so far, the posterior probability of guilt can still be anything at all: we need the prior probability in order nail down the posterior probability. The prosecutor's fallacy blithely assumes instead that P(h|e) = P(e|h). This may arise because conditional probabilities are often read as "if-then" conditional statements, and these are tricky and easily misread as their reversals. (See, for example, Kahneman and Tversky's work on "base rate neglect".)
Rather than ignore the prior here, however, we should estimate it. The question is something like: how often do mothers murder their first two children within their first year of life? We can answer a more general question, namely how often do mothers kill one or more of their children, of any age. Using this, of course, means we will be overestimating the prior probability by some unknown, but likely large, amount, implying that we are only finding an upper bound to the probability of interest. A news report suggests there are about 100 cases a year in the United States, estimated from surveys of prison populations. Since there are about 120 million adult women in the United States, and about half of them have children, that yields 1 in 600000 murdering their children in any given year. The homicide rate in the US is about 4 times higher than that in the UK (judging by this table), so that gives us 1 in 2.4 million. Of course, a mother may murder her children over the course of many years, but she cannot do so in a way that resembles SIDS beyond the child's first year. She might well get caught over the course of a few years, but using the annual figure alone is almost certainly not as big a factor for underestimating the probability of guilt as counting all cases of mothers killing their children works in favor of overestimating that probability. This way of getting a prior probability is admittedly crude, but it is nevertheless far better than that used by the prosecution, namely ignoring the issue of the prior altogether! Using our assumptions above we have enough to work Bayes' theorem:

 

  • P(h|e1 \wedge e2) = \dfrac{P(e1 \wedge e2|h)P(h)}{P(e1 \wedge e2|h)P(h) + P(e1 \wedge e2|\neg h)P(\neg h)}
  • P(h|e1 \wedge e2) = \dfrac{1 \times 1/2.4M}{(1 \times 1/2.4M) + (1/14.7M \times (1 - 1/2.4M))} \approx 0.86
This is a fairly high probability of guilt. However, if we were to routinely incarcerate people with a 14% chance of being innocent, we would be doing a lot of damage to society; "beyond a reasonable doubt" surely means that a higher standard is demanded. Some people (especially, some judges) think that the higher standard means certainty and that therefore probabilistic reasoning has no place in the courts. But ignoring probabilities is hardly the same as achieving certainty: it is simply a direct path to foolish decision making, such as that exemplified in the case of Sally Clark. Her case deserved a more serious treatment, including treatment of the relevant probabilistic facts. What actually happened was that an appeals court, despite being apprised of the probabilistic errors committed during the first trial, refused to overturn her conviction. Sally Clark was eventually found innocent after it came out that the prosecution had suppressed evidence showing that her second son died of natural causes. She subsequently died of alcohol poisoning.

Contrary to a widespread view in the legal community that statistical, and especially Bayesian, reasoning should not be considered in court proceedings, it is crucial in many cases that such reasoning be used — but, of course, used correctly. Many people find correct statistical reasoning difficult, but there are ways and means of improving it, some of which we will discuss in this blog. Meanwhile, if you are interested in Bayes and the Law, you might want to take a look at Norman Fenton's project.

† I thank Professor Philip Dawid for bringing this case to my attention and for helpful comments on it. His testimony to the appellate court on this case can be read here.

‡ This is so despite the widespread counselling of parents to the contrary and claims by various studies indicating no increased risk to siblings of SIDS victims! These studies all take pains to control for the kinds of risk factors I've identified above. What is relevant here is the increased risk of SIDS regardless of the cause (excepting those that Meadows actually did control for), and so the risk without controlling for alcohol, etc. is what is of interest. That risk, of course, is increased by the occurrence of a SIDS case in the family (observing an effect of a cause raises the probability of another effect being present!). The contrary claim, by the way, is probably put to parents as a means of reassurance; however, it could easily lead to complacency and to a neglect to deal with the risk factors in place in a family — in other words, made without qualification, the advice is both wrong and irresponsible.